دلتاس

سيستم مختصات و انواع آن

اين مختصات اغلب به گونه‌اي انتخاب مي‌شود كه هر يك عدد بيانگر موقعيت عمودي و دو يا سه عدد بيانگر موقعيت افقي باشد؛ از سوي ديگر، يك موقعيت جغرافيايي ممكن است با يك مختصات مركب سه بعدي بردار دكارتي بيان شود. در اين سه‌گانه ρ (رو) معادل r در سيستم مختصات قطبي است، θ (تتا) نيز مشابه سيستم قطبي است كه زاويه گِرايي يا آزيموت ناميده مي‌شود و φ (في) زاويه از سمت الراس (زنيت) است كه زاويه سمت الراسي ناميده مي‌شود. در هندسه، يك سيستم مختصات يك سيستم است كه از يك يا چند عدد و يا مختصات براي تعريف منحصر به فرد موقعيت نقاط و يا ساير عناصر هندسي روي يك خمينه (manifold) مانند فضاي اقليدسي، استفاده مي‌كند.

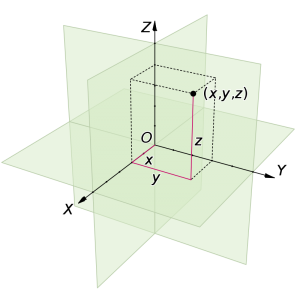
سيستم مختصات كروي يك گام جلوتر رفته و يك جفت از مختصات سه‌گانه استوانه‌اي (r, z) را به مختصات قطبي تبديل كرده است كه يك مختصات سه‌گانه (ρ, θ, φ) تشكيل مي‌دهند. در سيستم مختصات استوانه‌اي، يك مختصات z با معناي مشابه در مختصات دكارتي به r و θ در مختصات قطبي اضافه مي‌شود كه يك سه‌گانه (r, θ, z) را تشكيل مي‌دهد. مختصات در رياضيات ابتدايي اعداد حقيقي محسوب مي‌شوند، اما ممكن است اعداد مختلط و يا عناصر يك سيستم انتزاعي‌تر مانند حلقه جابه‌جايي باشند. يك سيستم مختصات جغرافيايي يك سيستم مختصات است كه تعريف هر مكان بر روي كره زمين را با مجموعه‌اي از اعداد، حروف و يا نماد‌ها ممكن مي‌سازد.

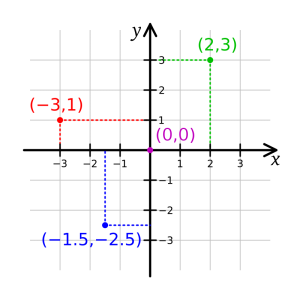
سيستم مختصات يكي از مفاهيم بسيار مهم در جغرافيا است كه پايه تمام نقشه‌ها و محاسبات مكاني است كه ريشه در علم هندسه دارد. در يك زاويه مشخص (θ) تنها يك خط از قطب مي‌گذرد كه زاويه آن با محور قطبي θ (تتا) باشد (به صورت پادساعت‌گرد محاسبه مي‌شود). ترتيب عناصر مختصات مهم است و گاهي توسط موقعيت خود در يك تاپل مرتب شده و گاهي توسط يك حرف مانند x-coordinate شناسايي مي‌شوند. براي اطلاع بيشتر پيرامون سيستم مختصات جغرافيايي پيشنهاد مي‌كنم مقاله بيضوي مرجع (بيضوي مبنا) چيست؟ را بخوانيد. كاربرد سيستم مختصات اجازه مي‌دهد مسائل هندسي به مسائل عددي ترجمه شوند و بالعكس؛ كه اين اساس هندسه تحليلي است.

منبع